Logikk og argumentasjon
Logikk er studiet av resonnementer.
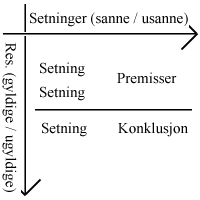
Et resonnement er gyldig hvis, og bare hvis, det ikke finnes noe annet resonnement på samme logiske form som har sanne premisser og usann konklusjon.
De setningslogiske termene:
- Og
- Eller
- Ikke
- Hvis (så)
- Bare hvis (så)
- Hvis og bare hvis (så)
En atomær setning er en setning som ikke inneholder setningslogiske termer.
1.1.2 Et resonnement setningslogiske form.
Et resonnements setningslogiske form fremkommer når vi beholder resonnementets setningslogiske termer og erstatter de atomære setningene med små bokstaver langt ute i alfabetet (p, q, r, ...)
Noen viktige setningslogiske resonnementsformer:
|
|
Hvis p, så q | Hvis antecedenten, så konsekventen |
| p | ||
| q |
|
|
Hvis p, så q |
| ikke q | |
| ikke p |
|
|
Hvis p, så q |
| * Ugyldig | q |
| p |
|
|
Hvis p, så q |
| * Ugyldig | ikke p |
| ikke q |
Eksempel. Skal vise at modus ponens er gyldig. (Hvis p, så q / p / q). Tar utgangspunkt i å prøve å vise at den er ugyldig. Mislykkes forsøket, er den gyldig.
For at et resonnement skal være ugyldig, må det være mulig å ha sanne premisser og usann konklusjon. Vi går derfor ut i fra:
| Hvis | p | så q | s |
| p | s | ||
| q | u |
| Hvis | ps | så qu | u |
| ps | s | ||
| qu | u |
|
|
|
|
| 1) s | s | s |
| 2) u | u | s |
| 3) u | s | s |
| 4) s | u | u |
Når har han ikke brutt sitt "løfte"?
1) Han kommer (s). Det blir kurs (s). Res. (s).
2) Han kommer ikke (u). Det blir ikke kurs (u). Res. (s). Han har ikke brutt løftet, det var bare i tilfelle han KOM han LOVTE det skulle bli kurs.
3) Han kommer ikke (u). Det blir kurs (s). Res. (s). Han har fremdeles ikke brutt sitt løfte. Han så bare at hvis han kom, ble det kurs. Ikke dermed sagt at det ikke ble kurs hvis han ikke kom. Han kunne f.eks. sende en vikar.
4) Han kommer (s). Det blir ikke kurs (u). Res. (u). Han har brutt løftet.1.1.4.2
| (far sover | og | mor leser) | |
|
|
|
|
|
| s | & | s | s |
| s | & | u | u |
| u | & | s | u |
| u | & | u | u |
De predikatlogiske termene:
- (og, eller, ikke, hvis, bare hvis, hvis og bare hvis)
- alle
- noen
- ingen
- (er)
Et resonnements predikatlogiske form fremkommer når vi beholder resonnementets predikatlogiske og setningslogiske termer og erstatter alle singulære termer med små bokstaver i begynnelsen av alfabetet (a, b, c, ...) og alle generelle termer med store bokstaver litt ut i alfabetet (F, G, H, ...)
Et resonnement er gyldig hvis, og bare hvis, det ikke finnes noe annet resonnement på samme logiske form som har sanne premisser og usann konklusjon.
| Alle fiskere er hester | u |
| Alle hester kan synge | u -- logisk gyldig resonnement |
| Alle fiskere kan synge | u |
| Alle F er G | (Alle fiskere er hester) |
| Alle G er H | (Alle hester er synge-kapable) |
| Alle F er H | (Alle fiskere er synge-kapable) |
Et holdbart resonnement er et gyldig resonnement med sanne premisser.